Exploring the World of Small Language Models (SLMs)

Keerthi Ganesh

AI/ML Developer

18 min read

Tags:

SLMs AI efficiency NLP

Small Language Models (SLMs) are revolutionising the field of natural language processing (NLP) by offering efficient, cost-effective, and highly capable alternatives to larger language models (LLMs). Let's delve into what SLMs are, their advantages, technical specifics, and applications.

What are Small Language Models?

SLMs are compact versions of language models designed to perform specific tasks efficiently while consuming fewer computational resources. They are engineered to provide powerful NLP capabilities on devices with limited processing power, such as smartphones, IoT devices, and edge computing environments.

Examples of Small Language Models (SLMs)

• Orca 2: Developed by Microsoft, Orca 2 is a fine-tuned version of Meta's Llama 2, utilising high-quality synthetic data. This innovative model achieves performance levels that rival or surpass those of larger models, particularly in zero-shot reasoning tasks.
• Phi 2: Phi 2, another model by Microsoft, is a transformer-based Small Language Model engineered for efficiency and adaptability in both cloud and edge deployments. It excels in areas such as mathematical reasoning, common sense, language understanding, and logical reasoning.
• DistilBERT: DistilBERT is a streamlined, more agile, and lightweight version of BERT, a pioneering model in natural language processing (NLP). It is designed to offer similar capabilities with fewer resources.
• GPT-Neo and GPT-J: These models are scaled-down versions of OpenAI's GPT models, providing versatility in application scenarios with more limited computational resources.

Advantages of SLMs

• Resource Efficiency: SLMs require significantly less memory and processing power, making them ideal for deployment on low-capability devices.
• Faster Inference: Due to their smaller size, SLMs can process data and generate responses more quickly, which is crucial for real-time applications.
• Cost-Effectiveness: Reduced computational requirements translate to lower operational costs, providing an economical solution for businesses.
• Enhanced Privacy and Security: SLMs can operate offline, keeping data on the device, which enhances privacy and security, particularly important in regulated industries.

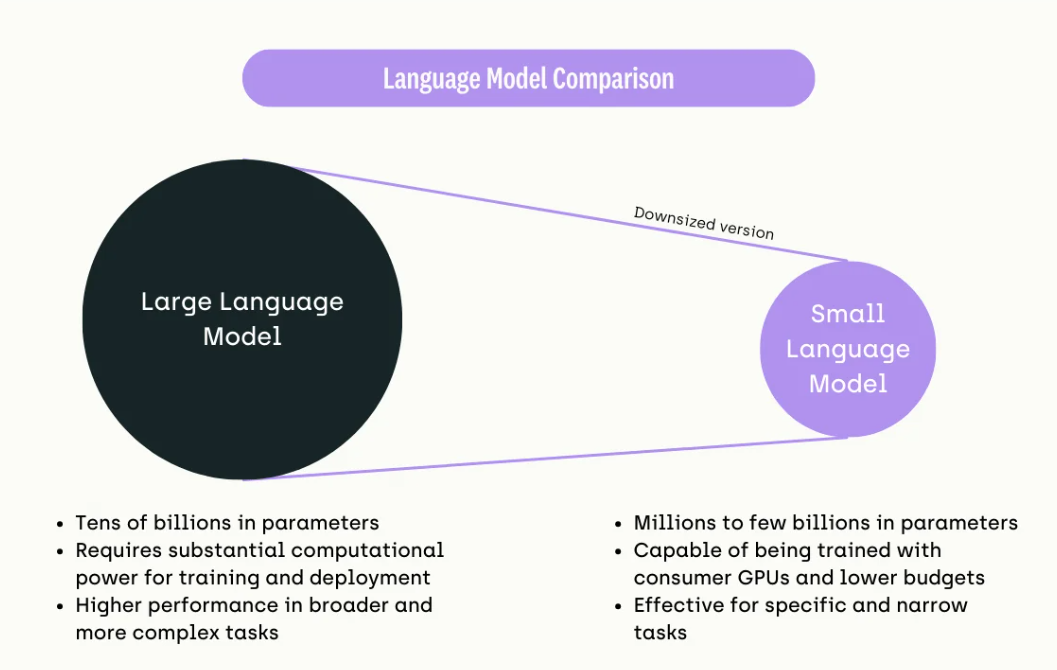
Small vs. Large Language Models: What Sets Them Apart

Small Language Models (SLMs) and Large Language Models (LLMs) serve different purposes in the realm of AI. Examines what sets them apart, detailing the critical factors that differentiate these models and their suitability for various applications.Here are ten primary distinctions:

• Size
  LLMs, such as Claude 3 and Olympus, boast an impressive 2 trillion parameters, whereas SLMs like Phi-2 have around 2.7 billion parameters. The vast difference in size significantly impacts their capabilities and applications.
• Training Data
  LLMs require extensive and varied datasets to meet broad learning objectives. In contrast, SLMs utilize smaller, more specialized datasets, making them suitable for focused and niche tasks.
• Training Time
  Training an LLM can take several months due to its complexity and the volume of data involved. SLMs, being less complex, can be trained within weeks.
• Computing Power and Resources
  LLMs demand substantial computing resources for both training and operation, consuming a lot of power. SLMs, while still resource-intensive, require considerably less computing power, making them a more sustainable option.
• Proficiency
  LLMs excel at handling complex, sophisticated, and general tasks due to their vast size and training. SLMs are more appropriate for simpler, more specific tasks where high proficiency isn't as critical.
• Adaptation
  LLMs are challenging to adapt for customised tasks, often requiring significant fine-tuning efforts. On the other hand, SLMs are easier to customise and fine-tune to meet specific needs and requirements.
• Inference
  LLMs need specialised hardware such as GPUs and cloud services to conduct inference, which often necessitates an internet connection. SLMs are compact enough to run locally on devices like Raspberry Pi or smartphones, enabling offline operation.
• Latency
  LLMs can suffer from high latency, especially noticeable in real-time applications like voice assistants, leading to slower response times. SLMs, due to their smaller size, typically offer quicker responses with lower latency.
• Cost
  The high computational demands of LLMs translate to higher token costs, making them expensive to run. SLMs, requiring less computational power, are more cost-effective to operate.
• Control
  With LLMs, you are dependent on the model builders, which can lead to issues like model drift or catastrophic forgetting if the model is updated. SLMs offer greater control, allowing you to run them on your servers, fine-tune them as needed, and freeze them to prevent changes.

Technical Insights

Recent advancements in SLMs, like Microsoft's Phi-3 models, have demonstrated that careful data selection and innovative training techniques can yield models that perform on par with much larger models. Here are some technical highlights:

• High-Quality Training Data: The performance of SLMs like Phi-3 is largely attributed to the use of "textbook-quality" data, which ensures that the models are trained on high-value, carefully curated datasets. This approach helps the models to understand and generate more accurate and contextually relevant responses.
• Efficient Architecture: Phi-3 models, for instance, employ Transformer-based architectures optimised for lower computational overhead while maintaining high performance. These models are instruction-tuned, meaning they are designed to understand and follow various instructions as humans would communicate, making them ready to use out-of-the-box.
• Scalable Deployment: SLMs can be deployed across different environments, including the cloud, edge devices, and even offline scenarios. This flexibility ensures that SLMs can be utilised in a wide range of applications, from mobile devices to autonomous systems.

Applications of SLMs

• Chatbots and Virtual Assistants: SLMs can power conversational agents, providing quick and relevant responses for customer support and personal assistance.
• Language Translation: They can handle basic translation tasks, offering real-time language conversion on devices with limited computational power.
• Text Summarization: SLMs effectively summarise long documents, extracting key information and presenting it concisely.
• Sentiment Analysis: Businesses can use SLMs to analyse customer feedback and social media posts, gaining insights into public sentiment with minimal computational overhead.

Future Directions:

While SLMs offer numerous benefits, challenges remain, such as limited capacity for understanding complex language patterns and reduced accuracy compared to LLMs. However, ongoing research is focused on enhancing their capabilities through better training algorithms and data selection techniques. Various models are a testament to how these improvements can lead to SLMs that rival much larger models in performance

Code Implementation :

Collab Link:SLM

Let's evaluate the Phi 3 mini SLM Vs GPT 4 turbo across various domains such as logical reasoning, mathematical problem-solving, ethical judgement and recommendation.

Install Required Libraries

                    
    !pip install git+https://github.com/huggingface/transformers
    !pip install accelerate
                    
                

Importing Libraries

                    
    import torch
    from transformers import AutoModelForCausalLM, AutoTokenizer, pipeline
                    
                

Loading the Model and Tokenizer

Load the pre-trained model and tokenizer. Here, we use Microsoft's Phi-3-mini-128k-instruct model.

                    
    model = AutoModelForCausalLM.from_pretrained(
        "microsoft/Phi-3-mini-128k-instruct",
        device_map="cuda",
        torch_dtype="auto",
        trust_remote_code=True,
    )
    tokenizer = AutoTokenizer.from_pretrained("microsoft/Phi-3-mini-128k-instruct")
                    
                

Defining Messages

Define the conversation messages between the user and the assistant.

                    
    messages = [
        {"role": "user", "content": "Can you provide ways to eat 
    combinations of bananas and dragonfruits?"},

        {"role": "assistant", "content": "Sure! Here are some ways to eat
    bananas and dragonfruits together: 1. Banana and dragonfruit smoothie: 
    Blend bananas and dragonfruits together with some milk and honey. 2. 
    Banana and dragonfruit salad: Mix sliced bananas and dragonfruits 
    together with some lemon juice and honey."},

        {"role": "user", "content": f"{query}"},
    ]                    
                    
                

Defining Generation Arguments

Initialise the text generation pipeline with the specified model and tokenizer.

                    
    pipe = pipeline("text-generation",model=model,tokenizer=tokenizer,)
                    
                

Defining Generation Arguments

Define the arguments for text generation. These control the behaviour of the generated output.

                    
    generation_args={"max_new_tokens": 500,"return_full_text": False,"temperature": 0.0,"do_sample": False,}
                    
                

Generating Responses

Use the pipeline to generate a response based on the defined messages ,query and generation arguments.

                    
    query="In a room, there are 5 people. Each person shakes hands with 
    every other person exactly once. How many handshakes occur in total? 
    Explain your reasoning."

    output = pipe(query, **generation_args)

    print(output[0]['generated_text'])
                    
                

Output

                    
    ### response: To solve this problem, we can use the concept of 
    combinations from combinatorics. A handshake involves two people, so we 
    are looking for the number of unique pairs of people that can be formed 
    from the group of 5.

    The formula for combinations is given by:

    \[ C(n, k) = \frac{n!}{k!(n-k)!} \]

    where \( n \) is the total number of items, \( k \) is the number of 
    items to choose, and \(! \) denotes factorial.

    In this case, \( n = 5 \) (the total number of people) and \( k = 2 \) 
    (since a handshake involves 2 people). Plugging these values into the 
    formula, we get:

    \[ C(5, 2) = \frac{5!}{2!(5-2)!} \]

    Calculating the factorials, we have:

    \[ 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 \]

    \[ 2! = 2 \times 1 = 2 \]

    \[ (5-2)! = 3! = 3 \times 2 \times 1 = 6 \]

    Now, we can substitute these values into the combination formula:

    \[ C(5, 2) = \frac{120}{2 \times 6} \]

    \[ C(5, 2) = \frac{120}{12} \]

    \[ C(5, 2) = 10 \]

    Therefore, there are 10 unique handshakes that occur in total.                        
                    
                

Question-Response Comparison Table:

Conclusion: The Promise of Small Language Models

Small language models (SLMs) like the Phi-3 Mini Model and other SLM’s offer a compelling blend of efficiency and performance. Despite their reduced size, these models demonstrate impressive capabilities in various areas such as reasoning, comprehension, creativity, and context understanding. The comparison between models shows that while there are subtle differences in their responses, small language models hold significant promise for a wide range of applications.

Their efficiency makes them accessible to a broader audience, requiring fewer computational resources without compromising the quality of output. This democratisation of AI technology allows more individuals and organisations to harness the power of language models without the need for extensive infrastructure. Furthermore, the versatility of these models enables them to be used effectively in numerous practical scenarios, from assisting in daily tasks to more complex problem-solving activities.

In conclusion, small language models are not just scaled-down versions of their larger counterparts; they represent a strategic approach to delivering powerful AI capabilities in a more resource-efficient and accessible manner. As the field of AI continues to evolve, the promise of small language models becomes increasingly evident, paving the way for innovative applications and broader adoption.

Back To Blogs

More Posts By This Author

Keerthi Ganesh

AI/ML Developer

AI/ML Engineer with a strong background in designing and implementing machine learning systems and algorithms.An Engineer who will demonstrate ownership and initiative in driving AI/ML initiatives forward, contributing to the advancement of our technology stack and business objectives.

Machine Learning Artificial Intelligence DataScience DeepLearning GenerativeAI Python

You may also like

Generative AI

OpenAI

LangChain

9 min read

Exploring the Role of Agents in AI: Leveraging LangGraph for Enhanced PerformanceL

Agents stand as pivotal components in the realm of Artificial Intelligence (AI), serving as autonomous entities tasked with executing functions...

Keerthi Ganesh

2024-03-11

PostgreSQL

6 min read

Evolution of JSONB - PostgreSQL

The evolution of JSONB in PostgreSQL has allowed for more efficient storage and querying of JSON data, making it a...

Akash

2023-01-16

React

6 min read

Code splitting (bundle-split) in React

Code splitting in React refers to the process of separating a large codebase into smaller, more manageable chunks or...

Navnit

2022-12-27

PostgreSQL

9 min read

Advanced SQL Part-4 | Window Functions Use Cases

In the Part 1 of this blog series, we learnt how to create a frame using frame_types - ROWS, RANGE and GROUPS...

Akash

2022-11-23